Properties of Real Numbers:
i. Commutative Property of Addition
a + b = b + a i______________________
…
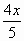 = 12x=_________
= 12x=_________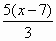
= 0 x=_________
- Recall, |a| = 7 means that a is either 7 or it is –7. Likewise, |a + 5 | = 7 means (a + 5) is equal to 7 or (a + 5) is equal to –7. This implies that a = 2 or a = -12. Solve for x:
- |x + 3| = 8x=_________
Coordinate System
- Determine whether the points given are solutions to the following equations, (i.e., does the point given lie on the graph of the equation?).
- y = 2x – 9(1, 2)Yes / No
- Find the length of the segment joining the given points, i.e. find the distance, d,
between the following points. Then find the midpoint, M, of the segment. Recall, d=
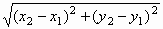 and M=
and M=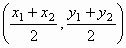
.
- (1, 2) & (4, 5).
- The point-slope form of a linear equation is y – y1 = m(x –x1). Using the point-slope form, write an equation of the line that passes through the given point P(x1, y1) and has the given slope, m. Simplify the equation and rewrite it in slope-intercept form, y = mx + b.
- P(1, 2) , m=½
- Using the point-slope form, write an equation of the line that passes through the given points (x1, y1) & (x2, y2). Simplify.
- (2, 3) & (4, 6) ______________
Inequalities with two variables.
- Graph the following inequalities.
- 3x + 2y ³ 12
- Given an equation of a parabola of the form, f(x) = y = a(x – h)2 + k, we have that (h, k) is the vertex …
Give the vertex of the following parabolas.
- y = x2 – 6x – 1 (_____,_____)
- Graph the following parabolas.
- y = x2 – 6x + 12
- Solve for the indicated variable.
- ax + by = c for xx=______________
- C = 2p r for rr=______________
- y = mx + b for bb=______________
- V = 2p r2 + 2p rhfor hh=______________
Exponents & Radicals
Some properties of exponents and radicals.
i. an × am = an+m …
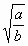 =
=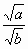
Example #4:
Simplify.
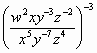 =
=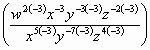 =
=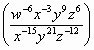 =
=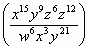 =
=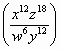 .
.
Example #5:
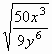 =
=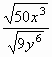 =
=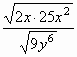 =
=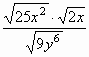 =
=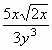
- Simplify.
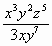 =______________
=______________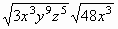 =______________
=______________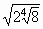
= ______________
Rationalizing
When working with radicals, we never leave a radical in the denominator of a fraction. …
- Solve.
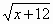 = 5x = _____________
= 5x = _____________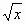 - 4 = 5x = _____________
- 4 = 5x = _____________- 5x – 30
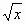
+ 45 = 0 x = _____________
Polynomials
Perfect Square Trinomials (a + b)2 = a2 + 2ab + b2
Difference of Squares a2 – b2 = (a + b)(a – b) …
- Add or Subtract the following polynomials by combining like terms.
- (x3 + 3x2 – 4x + 4) + (4x3 – 9x2 – 5x + 3)
- Multiply the following polynomials.
- (3x3 – x2 + 2x – 4)(x2 – 5x + 3) ____________________________________
- Expand (3x + 7y)2.____________________________________
- Factor completely:
- 2x2 – x – 6 ____________________________________
- Factor completely. (Hint: for some try using special formulas.)
- 49x2 – 25y2____________________________________
- (m2 + 18m + 81) – (n2 + 4n + 4)____________________________________
- Simplify.
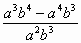 –
– 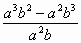
- _________________
Solving Rational Equations.
When solving rational equations, one must check answers for extraneous solutions. In other words, one must check to make sure the answers obtained are in the domain of the rational expressions (the denominator of the rational expressions cannot equal zero).
- Solve for x.
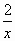 =
= 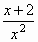
- x =______
Word Problems
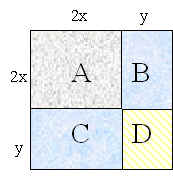
- Find the area of square A._____________________
- Find the area of rectangle C & D._____________________
Imaginary Numbers
i = ![]() i2 = (
i2 = (![]() )2 = -1 i3 = (
)2 = -1 i3 = (![]() )3 = (
)3 = (![]() )2(
)2(![]() ) = -1(
) = -1(![]() )= -i
)= -i
Zero Product Property
ab = 0 means a = 0 or b = 0.
I.e. if you have two numbers whose product is zero, one of them has to equal 0.
So, if given (x – 3)(x – 2) = 0, we have that a = x – 3 and b = x – 2 and either a or b equaling zero would make the product zero. Therefore, either
a = x – 3 = 0 or b = x – 2 = 0 which implies that either
x = 3 or x = 2.
This only works if the product ab = 0! If ab = 4, there are several numbers that can be multiplied to get 4 (2 and 2, 1 and 4, ½ and 8 to name a few). Therefore, it is vital that one does not make the following mistake:
x2 – 4x = 4
x(x – 4) = 4 means
x = 4 or x – 4 = 4 WRONG, WRONG, WRONG!
...
Factoring Tips …
Factoring by grouping:
Factoring using the "trial-and-error method."
Factoring using the "dream method"
Try it!
Factor 6x2 + 11x – 10 using both the trial and error method and the dream method.
Using Pascal’s Triangle to expand (a + b)n: …
Working with matrices.
The dimensions of a matrix are always given as "# rows x # columns." For,
example, the matrix  is a 3 x 2 matrix, while
is a 3 x 2 matrix, while ![]() is a 2 x 3 matrix. …
is a 2 x 3 matrix. …
Geometry is the study of points, lines, angles and all of the objects that can be made of points, lines, and angles. There are different kinds of geometries. In this book, we will study Euclidean geometry, also known as parabolic geometry. There are non-Euclidean geometries such as hyperbolic geometry and elliptic geometry. Other names of geometries include: projective geometry, spherical geometry, algebraic geometry, fractal geometry, etc.
Why are there so many different geometries? Each geometry deals with different characteristics and/or properties. In Euclidean geometry, one works with straight lines, circles, and arcs (fractions/parts of circles) which is fine if one is building a desk with straight lines or other objects we own.
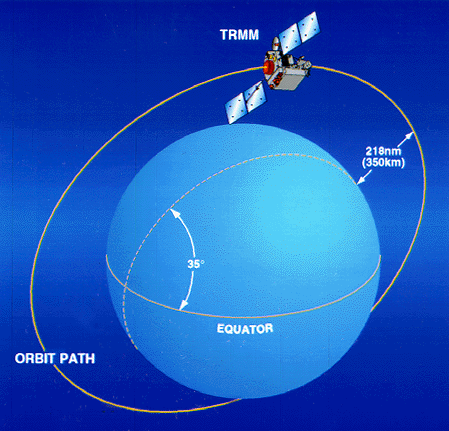
However, when we are working on the flight paths of our jet airliners, we need to work with a geometry without straight lines. Notice that airplanes do not travel in straight lines around the Earth, nor do satellites orbiting the earth, (see below). We would then work with a non-Euclidean geometry.

Images from NASA
- What is a geometry? _______________________________________________________________
- Why do we need different geometries? _________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
In order to well understand the other geometries, it is best to first grasp a strong understanding of Euclidean geometry.
SAN Problems (Sometimes Always Never Problems)
Directions: Write "S" in the blank if the statement given is sometimes true, "A" if the statement is always true, or "N" if the statement is never true. Sometimes it is helpful to use a penny as a point, a pencil as a line, and an index card for a plane to visualize the statements given. Rotate these objects and see if you can create the situations given with them.
- Three points are collinear.__________________
- Three points determine a plane.__________________
- Three non-collinear points determine a plane.__________________
- If two coplanar points determine a line, the line lies in the plane.__________________
- If one point is in a plane, a line passing through that point is also in the plane._________________
- Given a point and a line, one can draw a line through the point parallel to the line._____________